Beberapa blog yang penulis ikuti antara lain :
Blognya Kang Deni dengan alamat http://deni11math.wordpress.com, dan
Blognya Pak M. Yusuf dengan alamat http://labarasi.wordpress.com
sudah mengupas tuntas pembahasan soal OSN Matematika SMP tahun 2011. Beliau berdua tidak perlu diragukan lagi dedikasinya dalam upaya mengembangkan "Olimpiade Matematika" khususnya tingkat SMP di Indonesia melalui postingan-postingan soal, artikel, dan pembahasan-pembahasan soal yang cukup lengkap. Secara tidak langsung tulisan-tulisan beliau menginspirasi dan memotivasi penulis untuk juga ikut berpartisipasi demi kemajuan pendidikan di Indonesia khususnya dalam bidang matematika.
Tanpa berniat menggurui penulis mencoba memberikan alternatif pemecahan pada beberapa soal tersebut dengan menggunakan strategi dan pendekatan yang berbeda. Suatu strategi pemecahan masalah bisa jadi dapat mudah dipahami siswa tetapi belum tentu bagi siswa yang lain. Untuk itu siswa perlu dimotivasi untuk memecahkan masalah dengan berbagai strategi. Strategi mana yang terbaik biar siswa itu sendiri yang memutuskan.
Berikut pembahasan soal yang penulis maksud :
Soal Pilihan Ganda nomer 4
Seorang ilmuwan melakukan percobaan terhadap 50 ekor kelinci. dan melaporkan hasilnya sbb:
- 25 ekor diataranya kelinci jantan.
- 25 ekor dilatih menghindari jebakan, 10 ekor diantaranya jantan.
- 20 ekor(dari total 50 ekor) berhasil menghindari jebakan, 4 ekor diantaranya jantan.
- 15 ekor yang pernah dilatih berhasil menghindari jebakan, 3 ekor diantaranya jantan.
Berapa ekor kelinci betina yang tidak pernah dilatih, tidak dapat menghindari jebakan?
A. 5
B. 6
C. 7
D. 8
E. 9
PEMBAHASAN :
PEMBAHASAN :
Banyaknya kelinci = 50 ekor (25 jantan, 25 betina)
Misalkan n(S) banyaknya kelinci betina, maka n(S) = 25 ekor
Banyaknya kelinci yang pernah dilatih menghindari jebakan = 25 ekor (10 jantan,15 betina)
Misalkan n(A) banyaknya kelinci betina yang pernah dilatih menghindari jebakan, maka
n(A) = 15 ekor
Banyaknya kelinci yang berhasil menghindari jebakan = 20 ekor (4 jantan,16 betina)
Misalkan n(B) banyaknya kelinci betina yang berhasil menghindari jebakan, maka
n(B) = 16 ekor
Banyaknya kelinci yang pernah dilatih dan berhasil menghindari jebakan =
15 ekor(3 jantan, 12 betina)
15 ekor(3 jantan, 12 betina)
Maka banyaknya kelinci betina yang pernah dilatih dan berhasil menghindari jebakan adalah:
Sehingga,
Misalkan x banyaknya kelinci betina yang tidak pernah dilatih, dan tidak dapat menghindari jebakan , maka :
(Alternatif lain menentukan nilai x bisa menggunakan Diagram Venn. Silahkan dicoba!).
Jadi banyaknya kelinci betina yang tidak pernah dilatih, tidak dapat menghindari jebakan adalah
6 ekor
JAWAB : BJadi banyaknya kelinci betina yang tidak pernah dilatih, tidak dapat menghindari jebakan adalah
6 ekor
Soal Isian Singkat nomer 1
Lima permen identik (berbentuk sama). satu rasa apel. dua rasa jeruk dan dua rasa jahe akan dibagikan
Lima permen identik (berbentuk sama). satu rasa apel. dua rasa jeruk dan dua rasa jahe akan dibagikan
kepada lima sekawan Anto, Bono, Carli, Dodo dan Edo, sehingga masing-masing mendapat satu permen.
Peluang Anto mendapat permen rasa jahe adalah ...
JAWAB :
Banyak cara menyusun 5 permen dengan 1 rasa apel, 2 rasa jeruk, dan 2 rasa jahe adalah permutasi 5 unsur dengan ada unsur yang sama. Sehingga banyaknya ruang sampel adalah :
Jika Anto mendapat satu permen rasa jahe maka sisa 4 permen (1 rasa apel, 2 rasa jeruk, dan 1 rasa jahe) harus dibagi kepada 4 kawannya. Banyak cara menyusun adalah permutasi 4 unsur dengan ada unsur yang sama. Sehingga banyaknya kemungkinan adalah :

Jadi peluang Anto mendapat permen rasa jahe adalah

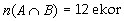


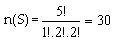
4 komentar:
Terima kasih banyak atas penjelasannya
Pak minta soal OSP matematika SMA 2011. Trimakasih
Maaf Mas Tutur, saya ndak punya. Ntar klo dapat Insya Allah tak kasih.
Pak Saiful pembahasan soal olimpiade tahun 2011 saya ambil, terima kasih, lain kali disambung lagi
Posting Komentar